根据维基百科，蒙特卡洛积分法是基于随机数的数值积分方法，用于计算定积分。对于高维的积分该方法具有巨大优势，因为蒙特卡洛方法是基于随机采样的方法，而很多其他方法是基于grid的，即将空间分割为不同的grid，最终将每个grid中的计算结果汇总，在n维的情况下这些方法就是O(n)的空间复杂度，而蒙特卡洛仍为O(1)，但要达到相同的精度，所需要的采样数量是否一定优于grid的方法，我暂时还未得到证明。

1. 算法说明

那么接下来我们来看看蒙特卡洛积分描述了怎样一个过程。
以一维的定积分$\int_{a}^{b}f(x)dx$为例，我们去找一个分布，其概率密度为：

$pdf(x)=\left\{ \begin{array}{cccc} p(x) & x\in (a, b) \\ 0 & else \end{array}\right.$ 那么在该分布上的$f(x)$的期望为： $E[f(x)]=\int_{a}^{b}f(x)p(x)dx$ 离散化后即可以有： $E[f(x)]\approx \frac{1}{n}\sum_{i=1}^{n}f(x_i)$ 其中$x_i$是按照$pdf(x)$采样出的某一样本。到现在可以看到我们距离目标积分，只差把$p(x)$消除掉。考虑定义函数$g(x)=\frac{f(x)}{p(x)}$，在该分布下$g(x)$的期望则是： $E[g(x)]=\int_{a}^{b}f(x)dx\approx \frac{1}{n}\sum_{i=1}^{n}\frac{f(x_i)}{p(x_i)}$ 综上所述，我们只要找到一个在该定义域上的分布，并且按照该分布采样多个样本$\{x_i\}^n$，最终将计算值求平均即得到该定积分的近似解： $\int_{a}^{b}f(x)dx\approx \frac{1}{n}\sum_{i=1}^{n}\frac{f(x_i)}{p(x_i)}$

2. 例子

一个比较常见的蒙特卡洛方法即投点法，如下图的rejective方法（取自维基百科）：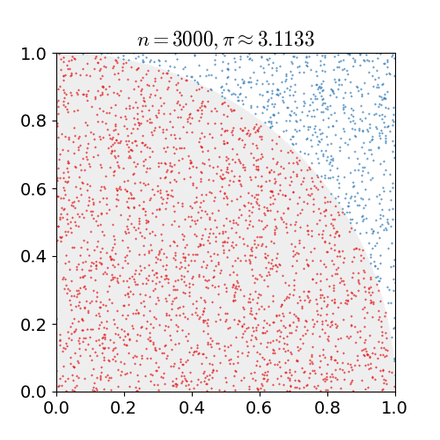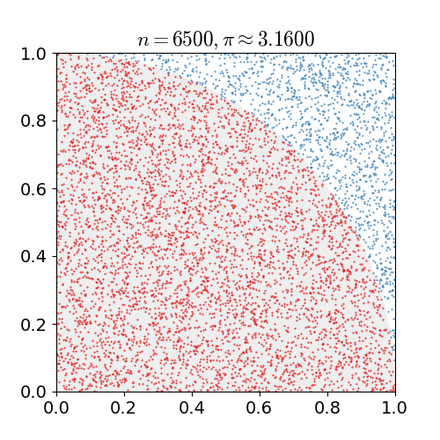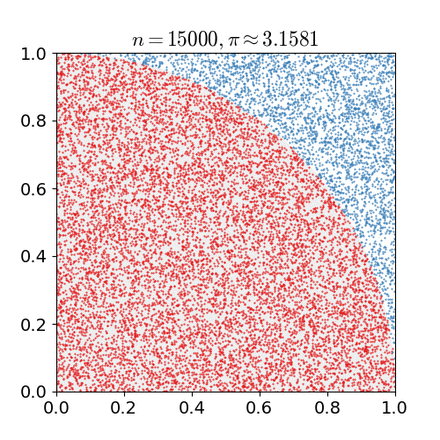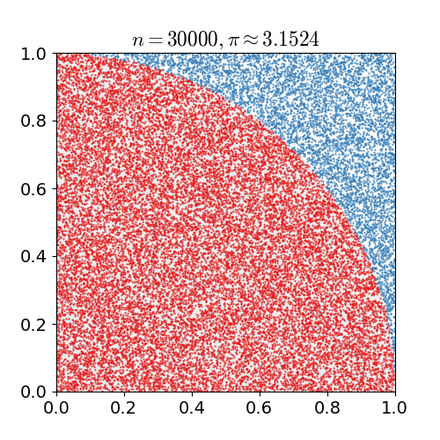
sphere
那么怎么用上述推导来解释这个过程呢。我这里给了一个可能的解释，首先可以定义一个二维函数$f(x,y)$:

$f(x,y)=\left\{ \begin{array}{cccc} 1& x^2+y^2 \le 1\\ 0 & else \end{array}\right.$
那么红色部分的面积即为$\iint_{D}f(x,y)dxdy$，其中$D$为正方形区域。那么投点做了什么事呢——在正方形区域中均匀采样，故$pdf(x,y)=1$，所以可以得到：

$\iint_{D}f(x,y)dxdy\approx \frac{1}{n}\sum_{i=1}^{n}\frac{f(x_i)}{pdf(x_i)} = \frac{1}{n}\sum_{i=1}^{n}f(x_i)$
这个求和即为：若采样点落在圆中，则计数加一，否则reject。

3. 重要性采样

关于重要性采样的在蒙特卡洛积分中的作用，我们可以看如下这个半球面积分的例子：

$\iint_{\Omega}cos\theta d\theta$
如果在半球面上进行均匀采样，蒙特卡洛方法如下：

$\iint_{\Omega}cos\theta d\theta=\iint_{\Omega}\frac{cos\theta}{\frac{1}{2\pi}}\frac{1}{2\pi} d\theta\approx \frac{2\pi}{n}\sum_{i=1}^{n}cos\theta$
而如果进行Cosine Weight的采样，则有如下结果：

$\iint_{\Omega}cos\theta d\theta=\iint_{\Omega}\frac{cos\theta}{\frac{cos\theta}{\pi}}\frac{cos\theta}{\pi} d\theta\approx \frac{\pi}{n}\sum_{i=1}^{n}1$
可以看到当我们的分布的概率密度刚好与$f(x)$差一个常数倍的话，我们甚至只需要采样一次。因此当分布于函数越相近时，我们所需要的采样数也就越少。