法向量变换 Normal Transformation

  在绘制物体的过程中，我们常常需要对物体的形状、位置等进行变换，从而可以从物体空间变换到世界空间，进而变换到相机空间，这些过程我们都可以通过矩阵乘法进行实现。对于点本身的位置$\textbf{p}$，假设我们有变换$\textbf{M}$，那么变换后的点位置为：

$\textbf{p'}=\textbf{Mp}$

  对于切向量，由于其可以视为切平面上的一点，与模型中的点位置变换是一致的，于是可以对切向量$\textbf{t}$做相同的变换：

$\textbf{t'}=\textbf{Mt}$

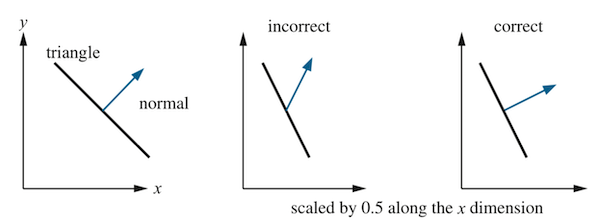
  但对于法向量来说，若我们直接应用相同的变换，在诸如放缩的操作后，可能出现如下的情况：

  令变换前的切向量和法向量分别为$\textbf{t}$和$\textbf{n}$，以及变换后的结果分别为$\textbf{t’}$和$\textbf{n’}$，那么希望有：

$\textbf{n'}^T\textbf{t'}=\textbf{n}^T\textbf{t}=\textbf{0}$
  已知$\textbf{t}$的变换为$\textbf{M}$，假设对$\textbf{n}$的变换为$\textbf{G}$，那么有：

$\textbf{n'}^T\textbf{t'}=\textbf{(Gn)}^T\textbf{(Mt)}=\textbf{n}^T\textbf{G}^T \textbf{Mt}=\textbf{0}$
  于是可以预见的一个解为$\textbf{G}^T \textbf{M}=\textbf{I}$，可以得到：

$\textbf{G}=(\textbf{M}^{-1})^T$
  但该方法要求$\textbf{M}$可逆，以及该变换不保证向量长度不变，因此可能需要归一化。另一种方法是计算法向量端点位置$\textbf{p}_1$、$\textbf{p}_2$，分别进行变换，再计算变换后的结果$\textbf{p’}_2-\textbf{p’}_1$。
  并且对于平移我们是不必在乎的，所以可以只关注左上角3*3的部分。若变换只包含旋转和平移，我们也可以直接应用原变换，并且不需要重新归一化。