lookAt() 函数

在OpenGL中我们可以借助gluLookAt()或glm::lookAt()函数设置或者获取相应的视角转换矩阵，从而将片元从世界坐标系转换到相机坐标系。接下来我们以glm::lookAt()为例讲述这一过程具体是如何实现的。首先我们可以看一下glm::lookAt()的函数声明：

template<typename T, qualifier Q>
GLM_FUNC_QUALIFIER mat<4, 4, T, Q> lookAt(
    vec<3, T, Q> const &eye, 
    vec<3, T, Q> const& center, 
    vec<3, T, Q> const& up
);

容易看出这是一个函数模板，接受三个三维向量，分别代表相机的位置eye、观察点center、朝上的方向up，并返回一个视角转换矩阵。在讲述原理前，我们先说明一下OpenGL中通常使用的坐标系。
如下图所示，在OpenGL中，我们通常使用右手坐标系 $\textbf{O}xyz$ ，即$\textbf{z}=\textbf{x}\times \textbf{y}$，并且希望经过视角变换后相机看向$-\textbf{z}$方向，并且相机朝上方向为$\textbf{y}$，即下图所示的$\textbf{O}ruv$: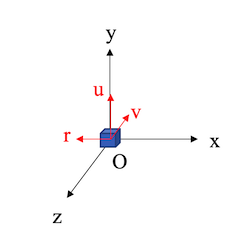
axis

接下来即可考虑如何根据三个输入参数eye、center、up获取上述转换矩阵。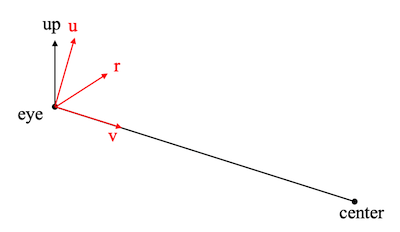
world
在上面的场景中，我们先根据三个输入参数计算世界坐标系下的三个相互正交的轴（需要说明的是输入参数up未必与视线垂直，因此需要校准）：

$\textbf{v} = normalize(\textbf{center} - \textbf{eye}) \\ \textbf{r} = normalize(\textbf{up} )\times \textbf{v} \\ \textbf{u} = \textbf{v}\times \textbf{r}$ 然后即是将eye平移到坐标系原点，令$\textbf{t}=-\textbf{eye}$，则有平移矩阵： $\textbf{R}=\left[\begin{array}{cccc} 1 & 0 & 0 & t_x \\ 0 & 1 & 0 & t_y \\ 0 & 0 & 1 & t_z \\ 0 & 0 & 0 & 1\end{array}\right]$ 继续将三个轴变换到相应的位置即可，看到如下每一行分别与$\textbf{r}$点积j的结果刚好为$[-1,0,0]$，达到了我们希望将该坐标系变换到上述的位置。（前提是三个轴两两正交） $\textbf{R}=\left[\begin{array}{cccc} -r_x & -r_y & -r_z & 0 \\ u_x & u_y & u_z & 0 \\ -v_x & -v_y & -v_z & 0 \\ 0 & 0 & 0 & 1\end{array}\right]$

综上，转换矩阵为：

$\textbf{M}=\textbf{RT} = \left[\begin{array}{cccc} -r_x & -r_y & -r_z & -\textbf{r}\cdot\textbf{t} \\ u_x & u_y & u_z & \textbf{u}\cdot\textbf{t} \\ -v_x & -v_y & -v_z & -\textbf{v}\cdot\textbf{t} \\ 0 & 0 & 0 & 1\end{array}\right]$

可以通过如下代码进行验证（此处默认右手系，在GLM中可以自主选择左右手系：

#include <glm/glm.hpp>
#include <glm/gtc/matrix_transform.hpp>
#include <iostream>

using namespace std;

int main()
{
    glm::vec3 eye(1, 1, 1);
    glm::vec3 up(0, 1, 0);
    glm::vec3 center(0, 0, 0);

    glm::mat4x4 lookat = glm::lookAt(eye, center, up);
    for (int i = 0; i < 4; ++i)
    {
        for (int j = 0; j < 4; ++j)
        {
            cout << lookat[j][i] << '\t';
        }
        cout << endl;
    }
    cout << endl;

    glm::vec3 v = glm::normalize(center - eye);
    glm::vec3 r = glm::normalize(glm::cross(up, v));
    glm::vec3 u = glm::normalize(glm::cross(v, r));

    glm::vec3 t = -eye;
    t = glm::vec3(glm::dot(-r, t), glm::dot(u, t), glm::dot(-v, t));

    cout << -r[0] << '\t' << -r[1] << '\t' << -r[2] << '\t' << t[0] << endl;
    cout << u[0] << '\t' << u[1] << '\t' << u[2] << '\t' << t[1] << endl;
    cout << -v[0] << '\t' << -v[1] << '\t' << -v[2] << '\t' << t[2] << endl;
    cout << 0 << '\t' << 0 << '\t' << 0 << '\t' << 1 << endl;
    return 0;
}

参考文献：
Real Time Rendering (4th edition)