1. 简单的想法

一般来说我们可以很容易写出绕坐标轴$x,y,z$旋转任意角度$\theta$的旋转矩阵，这里分别用$\textbf{R}_x(\theta), \textbf{R}_y(\theta), \textbf{R}_z(\theta)$来表示。但更多时候，我们希望给出任意轴$\textbf{r}$和任意角度$\alpha$的旋转矩阵$\textbf{X}$。一个简单的想法即将$\textbf{s}$构成的局部坐标系$Orst$变换到$Oxyz$上，然后应用相应的旋转，最后反变换回去，如下图所示：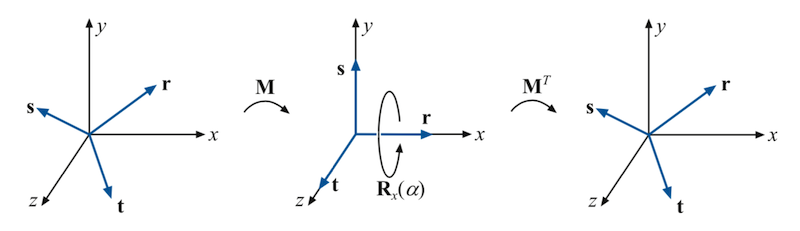
axis_rotation

首先我们计算$\textbf{M}$，按照Real-Time Rendering (4th Edition)中，一个比较稳定的方法即将绝对值最小值置零，然后交换剩下的值并将前一个值取负，可以验证该方法生成的向量与$\textbf{r}$垂直，只是需要进一步归一化，于是可以有：

$\overline{\textbf{s}}=\left\{\begin{array}{cccc} (0,-r_z,r_y) & if\ |r_x|\le|r_y|\ and\ |r_x|\le|r_z| \\ (-r_z,0,r_x) & if\ |r_y|\le|r_x|\ and\ |r_y|\le|r_z| \\ (-r_y,r_x,0) & if\ |r_z|\le|r_x|\ and\ |r_z|\le|r_y| \end{array}\right. \\ \textbf{s}=normalize(\overline{\textbf{s}}) \\ \textbf{t} = \textbf{r}\times \textbf{s}$ 对应的即可以得到$\textbf{M}$: $\textbf{M}=\left[\begin{array}{cccc} \textbf{r}^T \\ \textbf{s}^T \\ \textbf{r}^T \end{array}\right]$ 按照上述的坐标轴转换，最终的旋转矩阵即可以表示为： $\textbf{M}=\textbf{M}^T\textbf{R}_x(\alpha)\textbf{M}$

2. glm::rotate()

然而很容易发现该方案效率较低，需要多个计算，在glm::rotate()中，使用了Graphics Gems (1st Edition)中提到的另一种方法。该方法更直观地在旋转轴上进行操作，如下图所示。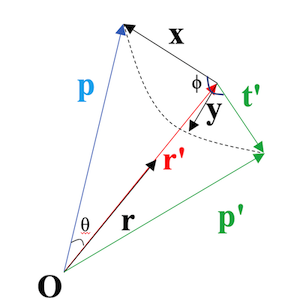
direct_rotation

首先我们有归一化的旋转轴$\textbf{r}$和任意需要旋转的点，这里用向量$\textbf{p}$表示，以及旋转角度$\phi$后的位置$\textbf{p’}$。如上图所示，我们将$\textbf{p}$投影到$\textbf{r}$上得到相应的投影向量：

$\textbf{r'}=||\textbf{p}||cos\theta\ \textbf{r} = (\textbf{p}\cdot\textbf{r})\textbf{r}$ 将$\textbf{x}=\textbf{p}-\textbf{r'}$作为旋转起始轴构建局部二维坐标系$\textbf{x}\textbf{y}$，那么在该局部坐标系下的旋转和最终的旋转结果即可表示为： $\textbf{t'}=cos\phi\ \textbf{x}+sin\phi\ \textbf{y} \\ \textbf{p'}=\textbf{r'}+\textbf{t'}=\textbf{r'}+cos\phi\ \textbf{x}+sin\phi\ \textbf{y}$ 上述已知$\textbf{r'}$，于是我们现在开始分别计算$\textbf{x}$，$\textbf{y}$： $\textbf{x}=\textbf{p}-\textbf{r'} =\textbf{p}- (\textbf{p}\cdot\textbf{r})\textbf{r} \\ \textbf{y} = \textbf{r}\times\textbf{p}$ 可以验证$||\textbf{x}||=||\textbf{p}||sin\theta=||\textbf{y}||$，然后将$\textbf{p'}$的计算式改写为： $\textbf{p'} = (\textbf{p}\cdot\textbf{r})\textbf{r}+cos\phi\ (\textbf{p}- (\textbf{p}\cdot\textbf{r})\textbf{r})+sin\phi\ \textbf{r}\times\textbf{p} \\ = cos\phi \textbf{p}+ (1-cos\phi)(\textbf{p}\cdot\textbf{r})\textbf{r}+sin\phi\ \textbf{r}\times\textbf{p} $ 接下来想办法将$\textbf{p}$提出来，剩下的算式组成的矩阵即是我们需要的旋转矩阵。在Graphics Gems (1st Edition)给出了如下的几个公式： $\textbf{p}=\textbf{Ip} \\ (\textbf{p}\cdot\textbf{r})\textbf{r} = \textbf{r}(\textbf{r}^T\textbf{p})=\left[\begin{array}{cccc} r_x^2 & r_xr_y & r_xr_z \\ r_xr_y & r_y^2 & r_yr_z \\ r_xr_z & r_yr_z & r_z^2\end{array}\right]\textbf{p}\\ \textbf{r}\times\textbf{p}=\left[\begin{array}{cccc} r_y p_z - r_z p_y \\ r_z p_x - r_x p_z \\ r_x p_y - r_y p_x \end{array}\right] = \left[\begin{array}{cccc} 0 & -r_z & r_y \\ r_z & 0 & -r_x \\ -r_y & r_x & 0 \end{array}\right]\textbf{p}$ 于是有： $\textbf{p'} = (cos\phi \textbf{I}+ (1-cos\phi)\left[\begin{array}{cccc} r_x^2 & r_xr_y & r_xr_z \\ r_xr_y & r_y^2 & r_yr_z \\ r_xr_z & r_yr_z & r_z^2\end{array}\right]+sin\phi\left[\begin{array}{cccc} 0 & -r_z & r_y \\ r_z & 0 & -r_x \\ -r_y & r_x & 0 \end{array}\right]) \textbf{p}$ 综上所述我们可以将该旋转矩阵表示为： $\textbf{M}=\left[\begin{array}{cccc} cos\phi+(1-cos\phi)r_x^2 & (1-cos\phi)r_xr_y-r_zsin\phi & (1-cos\phi)r_xr_z+r_ysin\phi \\ (1-cos\phi)r_xr_y+r_zsin\phi & cos\phi+(1-cos\phi)r_y^2 & (1-cos\phi)r_yr_z-r_xsin\phi \\ (1-cos\phi)r_xr_z-r_ysin\phi & (1-cos\phi)r_yr_z+r_xsin\phi & cos\phi+(1-cos\phi)r_z^2 \end{array}\right]$

参考文献

Real-Time Rendering (4th Edition)
Graphics Gems (1st Edition)